このうち二匹は一時間後の今も同じ位置のままですが、
他の二匹は互いに位置が入れ替わりました。
A「BはDのいたところに移りました」
B「DはAのいたところに移りました」
C「AはBのいたところに移りました」
D「Cは同じ位置のままではありません」
同じ位置のままの二匹はどちらもウソを述べていますが、
他の二匹が真実を述べているとは限りません。
いま、だれがどこにいるのでしょう。
こちらもおすすめです
>>111
CAが不動だとAの証言が本当になってしまう
CBが不動だとBの証言が本当になってしまう
CDが不動だとCの証言が本当になってしまう
DAが不動だとDの証言が本当になってしまう
DBが不動だとDの証言が本当になってしまう
よってCDは必ず動いていなければならず
、不動のカモシカはAB以外ありえない
答え
A、Bが動かずC、Dが入れ替わった
正解です
ある家族がいます。
この家族は舟を使って川の向こう岸へわたろうとしています。
舟は1艘(そう)しかなく、1度に2人まで乗ることができます。
家族は父、母、息子1、息子2、娘1、
娘2、メイド、犬の8人(犬も1人と数えます)であり、
またこの舟をこげるのは父か母かメイドの3人だけです。
さぁ、そしてこの家族、とっても危険な家族なんです。
まず父は、母がいないと娘を殺してしまいます。
また母は、父がいないと息子を殺してしまいます。
犬は、メイドがいないと家族をみんな殺してしまいます。
誰も死ぬことなく川をわたりきるにはどうすればよいでしょうか?
※カッコ内はその時点で対岸にいる者
①メイド、犬を乗せて対岸へ(メ、犬)
②メイド、ひとりで戻る(犬)
③メイド、娘1を乗せて対岸へ(メ、犬、娘1)
④メイド、犬を連れて戻る(娘1)
⑤母、娘2を乗せて対岸へ(母、娘1、娘2)
⑥母、ひとりで戻る(娘1、娘2)
⑦父、母の2人で対岸へ(父、母、娘1、娘2)
⑧父、ひとりで戻る(母、娘1、娘2)
⑨父、息子1を乗せて対岸へ(父、息子1、母、娘1、娘2)
⑩父、母の2人で戻る(息子1、娘1、娘2)
ここで完全に行き詰まるから無理じゃない?
出来るよ。
114だけど、これのっけたときにやっと解けた。
メイドが鍵。
そうか! たぶんわかった。
⑧までは>>115と同じで、
⑨メイド、犬を乗せて対岸へ(メ、犬、母、娘1、娘2)
⑩母、ひとりで戻る(メ、犬、娘1、娘2)
⑪父、母の2人で対岸へ(メ、犬、父、母、娘1、娘2)
⑫父、ひとりで戻る(メ、犬、母、娘1、娘2)
⑬父、息子1を乗せて対岸へ(メ、犬、父、息子1、母、娘1、娘2)
⑭メイド、犬を乗せて戻る(父、息子1、母、娘1、娘2)
⑮メイド、息子2を乗せて対岸へ(メ、父、息子1、息子2、母、娘1、娘2)
⑯メイド、ひとりで戻る(父、息子1、息子2、母、娘1、娘2)
⑰メイド、犬を乗せて対岸へ(メ、犬、父、息子1、息子2、母、娘1、娘2)
もちろん、父と母、息子と娘をともに入れ替えても可。
メイドは最初と最後の数回ずつしか
ボートを漕げないと思い込んでしまったので、
⑨が盲点になった…
無理ときめつけてハズカシー
川渡りパズル昔作ったなぁ。再出題してみようかな
昔からある問題だからすでに誰かが作ってるかもしれないけど
一応自分で作ってみた川渡り問題。
火竜(親1匹、子1匹)
氷竜(親1匹、子2匹)
水竜(親1匹、子2匹)がいる。
①船には一度にふたりまでしか乗ることが出来ない。
②船を運転できるのは親だけ。
③子竜のそばに親がいないとき
親火竜は子氷竜を、親氷竜は子水竜を、親水竜は子火竜を弱らせてしまう。
④竜同士は仲良しなので、親竜は自分の子竜はもちろん、他人の子竜も運べる。
(親火竜は子水竜を、親氷竜は子火竜を、親水竜は子氷竜を運ぶことができる)
子竜を弱らせることなく全員で川を渡るには最低何手必要か。
>>119はセンスいいな。
火竜:H,h 氷竜:K,k1,k2 水竜:M,m1,m2(それぞれ大文字が親)
として、条件③を整理すると、
・Hがいない場合、Mとh は同じ場所にいてはならない
・Kがいない場合、Hはk1, k2のどちらとも同じ場所にいてはならない
・Mがいない場合、Kはm1, m2のどちらとも同じ場所にいてはならない
(0)H,h,K,k1,k2,M,m1,m2|―|―
(1)K,k1,k2,M,m1,m2|H,h→|―
(2)K,k1,k2,M,m1,m2|←H|h
(3)K,k1,k2,M,m2|H,m1→|h
(4)K,k1,k2,M,m2|←H|h,m1
(5)K,k1,k2,M|H,m2→|h,m1
(6)K,k1,k2,M|←H|h,m1,m2
(7)K,k1,k2|H,M→|h,m1,m2
(8)K,k1,k2|←H,h|M,m1,m2
(9)h,k1,k2|H,K→|M,m1,m2
(10)h,k1,k2|←K|H,M,m1,m2
(11)h,k2|K,k1→|H,M,m1,m2
(12)h,k2|←H,K|k1,M,m1,m2
(13)H,h|K,k2→|k1,M,m1,m2
(14)H,h|←K|k1,k2,M,m1,m2
(15)h|H,K→|k1,k2,M,m1,m2
(16)h|←H|K,k1,k2,M,m1,m2
(17)―|H,h→|K,k1,k2,M,m1,m2
の17手で渡れる。最短手数の証明は…無理
15手でできる方法がふたつあります。
もう少し考えてみましょう。
まじか…、
これだけ入り組んだ条件があって15手ってすごいな。
正解できるかどうかはわからないけど、
「15手解があるならそれが最短」という証明だけはできそう。
以下、その証明の概略。
2人乗りボートで8人を渡すという条件だけなら、
最短手数は13手で、その全工程は、
「2人で向こう岸に渡る」→「1人で戻る」を
最後までひたすら繰り返すことにより達成される。
それに反して、「1人で向こう岸に渡る」「2人で戻る」の
いずれかを行った場合、
それぞれ1回につき1往復分、工程が増える。
>>119の①~④のすべての条件から、
初手は「親火竜が子火竜を乗せて渡る」に限定される。
また、最終手も同様に、
「親火竜が子火竜を乗せて渡る」に限定される。
ということは、一度対岸に渡った子火竜は、
途中のどこかの段階で
出発点に戻っていなければならないが、
子火竜は自分で舟を漕げないので、
親火竜か親氷竜に乗せてもらって戻ったことになる。
したがって、正解には「2人で戻る」工程が少なくとも1回ある。
以上により、13手解は不可能で、
15手解があるならそれが最短である。
勘違いあったらごめん。
15手解のひとつがわかった。
>>121の記法で、
(1)K,k1,k2,M,m1,m2|H,h→|―
(2)K,k1,k2,M,m1,m2|←H|h
(3)K,k1,k2,M,m2|H,m1→|h
(4)K,k1,k2,M,m2|←H|h,m1
(5)K,k1,k2,M|H,m2→|h,m1
(6)K,k1,k2,M|←H,h|m1,m2
(7)H,h,K,k2|M,k1→|m1,m2
(8)H,h,K,k2|←M|k1,m1,m2
(9)H,h,K|M,k2→|k1,m1,m2
(10)H,h,K|←M|k1,k2,m1,m2
(11)H,h|K,M→|k1,k2,m1,m2
(12)H,h|←K|k1,k2,M,m1,m2
(13)h|H,K→|k1,k2,M,m1,m2
(14)h|←H|K,k1,k2,M,m1,m2
(15)―|H,h→|K,k1,k2,M,m1,m2
最短手数の証明(概略)は>>123
1「3はBだ」
2「1はCではない」
3「2はAではない」
123は、ABCDEのどれか。
>>128
たぶん解けたと思うけど
解き方があまりスマートじゃないような…
T=真、F=偽 として、
1の発言が真、2が偽、3が偽という組み合わせを
'TFF' のように表すとき、
1,2,3の発言の真偽の組み合わせは
次の8通りである。
①TTT ②TTF ③TFT ④TFF
⑤FTT ⑥FTF ⑦FFT ⑧FFF
なので、それぞれについて検討する。
①~④の場合、1の発言が真、すなわち、
3→B である。
水槽の魚の組み合わせは AB|CDE で、
同じ水槽の魚に関する発言のみが真なので、
Bである3について真実を述べている1は、Aでなければならない。
つまり、1の発言が真ならば、
A1,B3|CDE が確定する。
ところで、2の発言は1に、3の発言は2に言及しているが、
A1,B3|CDE であるから、これらはいずれも、
異なる水槽にいる魚に関する発言、すなわち偽でなければならない。
この時点で①~③の可能性が消えるので、
④について検討する。
④TFFの場合、
1発言により、A1,B3|CDE
2発言が偽なので、1→C
3発言が偽なので、2→A
となるが、これは明らかに矛盾しているので、④の可能性も消える。
つまり、1発言は偽であり、⑤~⑧のどれかが正しい。
<続く>
1発言が偽なので、3はBでなく、A,C,D,E のどれかである。
また、1発言が偽なので、1と3は別の水槽にいる。
ここまでは確定。
そこで、まず2発言が偽の場合、つまり⑦⑧について検討する。
2発言が偽なので、1→Cとなる。
3は1と異なる水槽にいるが、Bではないので、3→Aとなる。
2は1について偽の発言をしているので、
やはり1と異なる水槽にいるが、3がAなので、2→Bとなる。
すなわち、2発言が偽ならば、
A3,B2|C1,D,E となるが、
問題の条件から、1,2,3の中にDがいなければならないので矛盾する。
つまり、2発言は真であり、⑤⑥の可能性だけが残る。
まず⑤について検討する。
⑤FTTの場合、
2の1に関する発言が真、
3の2に関する発言が真なので、
1,2,3が同じ水槽にいることになるが、
1と3は別の水槽にいることがすでに確定しているので矛盾する。
⑤の可能性も消えたので、残る⑥を検討する。
⑥FTFの場合、
2発言が真なので、1はCではない。
3発言が偽なので、2→A
2発言が真なので、2は1と同じ水槽にいる。
すなわち、1→B
3発言が偽なので、3は2と異なる水槽にいる。
すなわち、3はC,D,Eのどれかであるが、
問題の条件から、1,2,3の中にDがいなければならないので、
3→D
答:1→B, 2→A, 3→D
>>130-131
正解です。
史上最強の論理パズルという本からの出題でした。
以下解法
1の発言が真実(3がB)とすると、1はA、2の発言が真実となるが、同じ水槽に2のいられる場所がないので、1は嘘で1と3は別の水槽にいる。
2が3と同じ水槽にいるとすると、2の発言により1はCで、2と3は1とは別の水槽なのでDの魚がいないことになる。ゆえに、2と1は同じ水槽。
これにより、正解が得られる。
「ほとんどの人が間違える問題」と書いてあったので、
息巻いていたらどこが引っ掛けなのかもわからないままに
解けてしまった拍子抜け問題。
ある男性が肖像画を見ていた。
「誰の絵を見ているのですか」
とこの男性に答えると、こう答えた。
「私には兄弟姉妹はいないが、この男性の父親は私の父親の息子だ」
この男性が見ているのは誰の絵か。
>>134
だよなぁ、間違えないよなぁ。
普通に考えて、自分の息子だよなぁ。
なんか、ほとんどの人は間違える。当たった人も説明できない。
この問題について数時間議論したとか書いてあって
は?って感じなんだけど。
この4人の間で席替えが行われた。4人の希望は次の通りだった。
A「Dのすぐ左はいや」
B「Dの隣はいや」
C「Aの隣はいや」
D「Bの隣がいい」
このうちの一人のみ願いがかなったときの、新しい席順は?
[B,C,A,D],[False,True,False,False]
[C,A,D,B],[False,False,False,True]
よくわからないのはAの態度だよねー
>>143
次どうぞ。
A,B,Cの3人が庭にいた。
そこに通りかかった人が、Aに「あなた方の中に正直者は何人いるか」と尋ねた。Aの答えは不明瞭だったので、尋ねた人はAが何と言ったのか分からなかった。そこでBに「Aはなんと言ったのか」を尋ねた。
Bは「Aは私たちの中に正直者は一人だけだ、と言ったのだ」と答えた。
するとCが「Bを信じてはいけない。嘘をついている」と言った。
BとCは嘘つきか、正直者か。
●Bが正直者の場合
Cは嘘つきに確定。
Aは「私たちの中に正直者は一人だけ」と言ったことになる。
Aの発言が真ならAは正直者だが、すると、正直者がA、Bの2人になり、
Aの発言は偽になってしまう。
Aの発言が偽ならAは嘘つきだが、すると、正直者はBだけになり、
Aの発言が正しくなってしまう。
いずれにしろ矛盾するので、Bは正直者でない。
●Bが嘘つきの場合
Cは正直者に確定。
Aについては、
「私たちの中に正直者は一人だけ」と言わなかった(それ以外のことを言った)
ということしかわからず、正直者か嘘つきかはわからない。
答:B=嘘つき、C=正直者
という解釈でいいのかな?
「Aは私たちの中に正直者は一人だけだ、と言った」という
Bの発言が嘘だという情報を、
Aは「私たちの中に正直者は一人だけではない」と言った
ととらえると、
A=正直者 まで確定できるけど、
その解釈にはちょっと無理があるように感じる。
でも、無理のある解釈のほうが題意のようにも思える。
>>151
Aについては解説がありませんでした。
私も、Aは正直者で確定では?と思ったのですが...
解説できる人いらっしゃったらお願いします。
確認しておきたいのですが、
「一人だけだ」の否定が「一人だけではない」だとすると、この表現には当然0人、2人、3人の可能性がそれぞれあるということで良いんですよね?
>>153
> 確認しておきたいのですが、
> 「一人だけだ」の否定が「一人だけではない」だとすると、この表現には当然0人、2人、3人の可能性がそれぞれあるということで良いんですよね?
そこが自然言語の厭らしい点ですね。
「一人だけだ」と「一人だ」とは数学言語では区別して表しようがありませんが
日常言語だと「一人だ」を否定した「一人でない」は人数が1人でなければOKなので勿論0人の場合も許します。
ところが「一人だけだ」の否定である「一人だけではない」という文が普通の日常の日本語の使用で表す意味は
「人数は複数だ」という文と同じ意味であって0人の場合は許されません。
この問題の場合、出題者が「一人だけだ」という言葉を用いた意図はどちらなのでしょうね?
単に(数学言語と同じく)「一人だ」というのと同じ意味で使うつもりだったのか、それとも上の日常の日本語の使用に照らした意味のつもりなのか?
解決しました。回答ありがとうございます。
本の著者がアメリカ人の数学者でしたので、
日本語に即した意味ではないと思われます。
違和感ありますが、数学的意味合いでしょう。
AとBはそれぞれ嘘つきか、正直者か。
>>156
これ面白いね。
「私は嘘つき」と言っている以上、
Aが正直者である可能性はないので、
Aは嘘つきなんだけど、そうきめるには、
「私は嘘つきだが、Bはそうではない」
という発言全体をひとまとまりにして考えなきゃいけない。
「私は嘘つきだが、Bはそうではない」
を言い換えると、
「私は嘘つきであり、かつ、Bは正直者である」
これが嘘なんだから、
Aが嘘つきでないか、Bが嘘つきであるかの
少なくともどちらかが成り立って
いることになる(ド=モルガンの法則)
しかし、Aは嘘つきなのだから、
Bは嘘つきでなければならず、
したがって、A、Bともに嘘つき。
これが一応の答え。
しかし、
Aの発言を「私は嘘つきだ」「Bは正直者だ」
というふうに分割してしまうと、
いわゆる『嘘つきのパラドックス』が生じる。
(正直者も嘘つきも「私は嘘つきだ」とは言えない)
それじゃ、Aがどんな言い方をすれば
パラドックスを免れるのか?
出題の「私は嘘つきだが、Bはそうではない」は、
ぎりぎりセーフかな? それともグレイゾーン?
「私は嘘つきだ。Bは違うけどね」
だったらもう、完全にアウトだよね?
「私は嘘つきであり、かつ、Bは正直者である」
と言えば余裕でセーフだけど、
普通、そんなしゃべり方する奴はいないし…。
正解です。
数学言語的にbutはないので、戸惑ってしまいますね。
では次の問題。
「ヴェニスの商人」のポーシャが肖像画を隠した小箱のパロディです
(説明面倒いので知らない人はggって)
金の小箱:肖像画は銀の小箱の中にない
銀の小箱:肖像画はこの小箱の中にない
鉛の小箱:肖像画はこの小箱の中にある
肖像画が入っているのは一体どれ?
ググって出た問題の条件は
①「三つの箱の内一つだけ真実が書いてある」、②「肖像画は一枚」だったが、
この場合、金と銀が同じ事を言っている為、金と銀は両方嘘か両方真実。
条件①が適用されるなら、両方嘘で鉛が真実となる。
しかしその条件を満たすには鉛に肖像画が入っていて、銀にも肖像画が入っている事になる。
すなわち答えは「銀と鉛、あるいは三つ全てに肖像画が入っている」となり、条件②に矛盾するが、まさかこれが答えじゃないだろう?
というか問題出すなら面倒でも条件ぐらい問題文にきちんと書けよ。
確かに条件ないのは困るよねー。
元ネタがあるにしても、パロディというからには
条件の部分もひねってある可能性があるわけだし…。
>>160の①の条件をはずして検討してみると、
金と銀に書いてあることは同じだから、
(1)金・銀・鉛 → 真・真・真
(2)金・銀・鉛 → 真・真・偽
(3)金・銀・鉛 → 偽・偽・真
(4)金・銀・鉛 → 偽・偽・偽
の4通りについて考えればよい。
>>160の②の条件は生きているとすると、
(1)の場合、肖像画は鉛の箱の中
(2)の場合、肖像画は金の箱の中
(3)の場合は、>>160の通り、
肖像画は銀の箱にも鉛の箱にもあることになり、条件②に矛盾
(4)の場合、肖像画は銀の箱の中
となり、何か条件を加えないと答えはでない。
試しに、条件①に代えて、
「ひとつの箱にだけ嘘が書かれている」という条件を与えてみると、
(2)に限定され、答えは「金の箱」となる。
しかし、金と銀に書いてあることが同じなのが
あからさまに見えているので、
問題としてはちょっと簡単すぎるかも。
>>160-161
ごめん、少なくとも一つは真、少なくとも一つは偽でした。
なので(2)が正解です。
では次の問題。
これらの3つの箱は、有名な職人であるチェリーニかベリーニの作である。ベリーニが作った小箱に刻まれた銘文は真、チェリーニが作った小箱に刻まれた銘文は偽である。そして、3つの小箱のうち1つに短剣が入っており、その箱を開けてはならない。
金の小箱:短剣はこの小箱の中にある
銀の小箱:この小箱の中には何もない
鉛の小箱:三つの小箱のうちベリーニの作は一つだけだ
どの箱を開ければ良いか
併せてこちらもどうぞ。条件は同じ。
金の小箱:短剣はこの小箱の中にある
銀の小箱:この小箱の中には何もない
鉛の小箱:三つの銘文のうち真は一つだけだ
・金の小箱の銘文が真なら、短剣は金の小箱にあるので、銀か鉛の小箱を開ければいい
・金の小箱の銘文が偽なら、
銀の小箱の銘文が真ではありえず、
金銀鉛=偽真真→鉛の小箱の銘文が偽になる、
金銀鉛=偽真偽→鉛の小箱の銘文が真になる
偽となるので、金か鉛の小箱を開ければいい
結局、鉛の小箱を開ければいい
…と思ったが、
金の小箱:偽(チェリーニ作)=短剣は金の小箱の中にはない
銀の小箱:偽(チェリーニ作)=この小箱の中には短剣でない何かがある
鉛の小箱:真(ベリーニ作)、短剣入り
だったらアウトだな
あと、163と164の違いがわからない
>>165
>>163と違い、>>164の問いは実はパラドックスとなります。
なぜ、パラドックスとなるのかを説明してください。
引っ掛けようとしてあえて詳しく書かなかったんですが
問題を解く人がいなくて(´・ω・ ` )
そのうちの一つには 短 剣 、他の二つは 空 です。
この熊は何色か。
黒 北極点に(●゚(エ)゚●)のぬいぐるみを置いていた。
>>178
まぁまぁ、正解ということで。
製作者は白と答えさせたかったんでしょうが。
解は無数にありますが、ここでは割愛。
次どうぞ。
見た目で区別のつかないAとBの兄弟がいる。この一方は、月・火・水曜日に嘘をつき他の曜日は本当のことをいう。また一方は、木・金・土曜日に嘘をつき他の曜日は本当のことをいう。あなたはこの事実を知っているが、どちらがどちらの曜日群に嘘をつくのかは知らない。
※この設定は引きずる予定
さて、この兄弟はあなたに出会うとこのように言った。
???「私はAだ」
???「私はBだ」
どちらがAでどちらがBであるか。
>>181
正解です。
すごくどうでもいいですが、問題文に自分を組み込まれるといらっとしますね。
次、どうぞ。
また別の日、兄弟の一人に会うと彼はこう言った。
「私はBで、今日私は嘘をついた」
これは誰か。
「私はBで、今日私は嘘をついた」全体が真だとすると
「私はB」「今日私は嘘をついた」の両方が真でなければならないが
「今日私は嘘をついた」は真になり得ないので矛盾
従って「私はBで、今日私は嘘をついた」は全体では偽
このためには「私はB」が偽で「今日私は嘘をついた」が部分的に真になればいい
だからA
…と思ったが、
>>157の「かつ」の問題があるし
「ついた」の過去形(?)も気になるところ
お察しの通り「かつ」の問題でしたが、正解です。
解答に過去形についての言及はなかったので、分かりませんが、
「今日私は嘘をつく」だと、文章として不自然ですし、「今私は嘘をついている」だとパラドックスになってしまうので、過去形になったのかと思います。
小学5年の娘の宿題がなかなか面白かったので出題させてください
きっとこのスレ民の叡智を持ってすれば瞬殺でしょうが、前菜代わりにドゾ
(頼まれて自分で解いてはみたものの、ホントに正解なのかチト不安なので…ってのはナイショw
リカさんは鳥を200羽くらい飼っています
友達に鳥の内訳を聞かれて、「1/3は南米産、1/4はアフリカ産、1/5は東南アジア産、1/7は中国産で1/9は北米産です」、と答えました
ところがリカさんは慌てていたので、一つ数字を間違えて答えてしまいました
さて鳥は何羽いるのでしょう?
>>258
3、4、5、7、9のうち4個で割り切れる正の整数で、200に最も近いのは180だから答えは180羽
(間違いの数字は1/7の分母の7で、正しくは、180の正の約数で羽数が180を超えない
10、12、15、18、20、30、36、45、60、90、180のいずれか)
どや
>>262
さすがです!
つまんない問題だから放置プレイかぁ…と諦めてました
1/7の代わりの正解の数がそんなに沢山あるのはちょっと盲点でした、1/10を思いついた時点で満足しちゃってましたw
余談ですが娘が先生に正解を聞いたところ、今は忙しいからまた今度ね!だったそうです
日本の未来が不安ですw
小学生にしてはこれ難しいと思うなw
てか学校で教えてこんな計算何に使うのかね。
すみません、論理パズルじゃないのですが、これ解ける人いますか?
3 2 1 7
6 5 4 9
9 4 5 5
8 4 8 6
4 2 ◇ 7
◇に入る数字はなに?
色々試したんですけど分からなくて、、
8
>>267
3|21|7
6|54|9
9|45|5
8|48|6
4|2◇|7
面白いね(´・ω・`)
しかし1枚だけ偽物です。
偽物は本物と重さが異なります。偽物以外は全て同じ重さです。
天秤秤を三回だけ使って偽物を見つけ出せ。
1回目
1~4を左皿に、5~8を右皿に載せる
重さが違う(1~8に偽物がある)→2回目Aへ
重さが同じ(9~13に偽物がある)→2回目Bへ
2回目A
1,2,3,5,6を左皿に、9~13を右皿に載せる
・天秤の傾きが1回目と同じ
1,2,3のどれかが偽物→3回目Aへ
・天秤の傾きが1回目と逆
5,6のどちらかが偽物→3回目Aへ
・重さが同じ
4,7,8のどれかが偽物→3回目Bへ
3回目A
2回目は右皿に本物だと確定しているものだけを載せて比べた結果なので
その傾きで偽物が本物より重いか軽いかも分かっている
よって、偽物だと疑われる物の中から1個ずつ選んで左右の皿に載せれば確定できる
3回目B
7を左皿に、8を右皿に載せる
・天秤の傾きが1回目と同じ→8が偽物
・天秤の傾きが1回目と逆→7が偽物
・同じ→4が偽物
2回目B
9,10,11を左皿に、1~8から3つ選び右皿に載せる
・重さが違う
9,10,11のどれかが偽物→3回目Aへ
・重さが同じ
12を左皿に、1~11から1つ選び右皿に載せる(3回目C)
重さが違うなら12、同じなら13が偽物
>>276
正解
カンニングした?
そうか、つまり君はそういう奴なんだな……
>>285
解けたよ。
ココ-バラ-4年前-10本(以下略)
2年前に植えたコスモスの次に…でひっかかってるのかも。
コスモスが一番多い=30本とは限らない。
ルナの本数何本?
ルナの本数が無くなるんだけど
追記だけど、一番多いのは五年前のアジサイになるんだけど
2年前のコスモス<レオ<五年前の花
なんだけど
この文章
ルナが四年前、三年前じゃない、1年前2年前より本数少ないって事でしょ?
そうするとルナは五年前になるけど
2年前コスモス<<レオ<<五年前(ルナ?)になってしまって矛盾する
ここを解説してくれると助かります
とりあえずコスモス>レオ>5年前(ルナ)な。
あーーー!!
解ったーー
ありがとうございます
俺が馬鹿過ぎて、勘違いしていた
一つの州からは、1個100㌘の金の棒数十本が税金として王宮に納められる
ある時密告で、某代官が1割少ない重さの延べ棒を鋳造しているという
王宮には秤がなくコインを入れて計るデジタル計量器を日本から輸入した、
しかし、問題があって王宮には料金として入れる100円玉が1個しか無い
さあ、1回で各州から集められた延べ棒のうち、どれが少ないのか調べてくれ
仮に10の州を1~10と番号を振り、
1の州から1本2の州から2本・・・10の州から10本。
計55本の重さを量る。
仮に50グラム少ない時は5番の州が犯人
真面目か
100円玉1枚あれば使うたびに回収して、また投入すればいいだけだ
教えてください、こういった問題はどんなアプローチで解けばいいんでしょう?
A~Dの4人がパーラーへ行きました、
パーラーでは、ケーキ、シュークリーム、パイの3種類のお菓子と
コーヒー、紅茶の2種類の飲み物がありました
Aは2種類のお菓子とコーヒーを注文
BはAと同じお菓子は注文しなかった
CはDと同じ飲み物を注文した
Dはシュークリーム以外のお菓子1つを注文した
1.シュークリームを注文したのは1人だけ
2.コーヒーは2人が注文した
3.Dはケーキを注文した
4.Cはシュークリームを注文した
5.Dはパイを注文した
Aは2種類のお菓子とコーヒーを注文
BはAと同じお菓子は注文しなかった
↓
AとBで3種類のお菓子を1個ずつ注文している
3人が同じお菓子を注文した
↓
AかBのどちらかと同じお菓子をCもDも注文している
Dはシュークリーム以外のお菓子1つを注文した
3人が同じお菓子を注文した
↓
Dが注文したのはケーキかパイのどちらか
よって3人(ACDあるいはBCD)が注文したのはケーキかパイのどちらか
Cが注文したのはケーキかパイのどちらか、あるいは両方
これより選択肢の3、5は確定できない
4は不適当
2は飲み物に関する条件がないので確定できない
1はAかBかのどちらか一人だけが注文しているので正しい
正しいかも知れないが、絶対に正しいとは条件から導けないってことか
う~ん、実際に解いてるときは文面からは矛盾しないと思っちゃいます
ありがとうございました
一袋だけ不在の三男に残し、残りを長男と次男で分けあう。
ただしビー玉は、袋に入った形でしか分けあう事ができない。
長男のビー玉数が次男の2倍になる組み合わせは、何通りあるか?
>>315
理詰めでいいのかこれ?
三男に18渡すと残りの総計が122になるから無理
同様に考えて
19渡しても121で無理
21渡しても119で無理
23渡した時は117なので
39と78に分ければ条件を満たす
18+21 と 19+25+34か
25渡すとこれまた残り計115なので無理
34も・・・残り106だから無理
答えは一通りだけか
>>317
140は3で割ると余り2です。
6つに袋のビー玉を「3で割った余り」が何なのか確認してみましょう。
18 ≡ 余り0
19 ≡ 余り1
21 ≡ 余り0
23 ≡ 余り2
25 ≡ 余り1
34 ≡ 余り1
よって23個の袋を三男に渡す、一通りのみ。
得点X、Y、Zは常に同じ値で、X>Y>Z>0を満たす整数である。
ゲームが全て終わり、Aは22点、Bは1回以上1位になり9点、Cは9点だった。
Cが2位になったのは何回?
解き方は?
1回のゲームで得られる点の合計もゲーム数も(22+9+9)の約数
x+y+z≧6
x≦9-(ゲーム回数-1)
Bが9点、Aが22点と成り得るのは(x,y,z)=(5,2,1)のとき
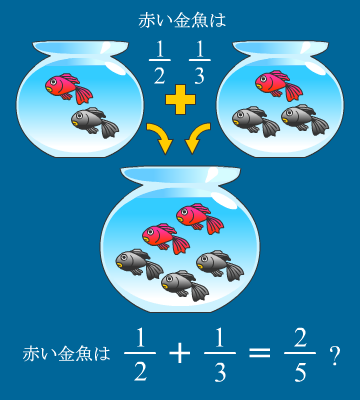
分数は「1をいくつかに分けたうちのいくつか」でなければならない
金魚に使われている表現は「何個中何個」を表す俗的な表現であって
そもそも分数ではない
つまり1に相当する匹数が袋毎にバラバラだから
単純に足し引きできないって事ね。